Übersicht
Mathematik
Physik
Chemie
Verfahrenstechnik
Geologie
Mikrobiologie
Elektrotechnik
Astronomie
Biologie
Hydrologie
Hydrogeologie
Wirtschaft
Statistik
Informatik
Regeltechnik
Zurück zur Homepage
Die einzelnen Fächer:
Mathematik
Geometrie
Algebra
Stochastik
Infinitesimalrechnung
Analytische Geometrie
Komplexe Zahlen
Sphärische Geometrie
Geometrie
Thales
Zentrische Streckung
Pythagoras
Höhensatz und Kathetensatz
Strahlensatz
Berechnungen mit unter anderem dem Sinus
Planimetrie
Stereometrie
Sinushyperbolicus
Thales
Hier folgt ein Java-applet, welches zu einem bestimmten Winkel den Kreisbogen berechnet, bei60° wäre es genau ein Halbkreis
Zentrische Streckung
Hier soll ein Java-applet kommen, welches ein gezeichnetes Objekt vergrößert oder verkleinert.
Pythagoras
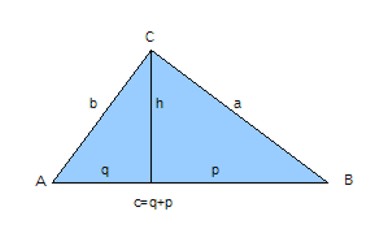
Höhensatz und Kathetensatz
Geben Sie nun die Werte der Hypotenusenabschnitte p und q ein!
siehe Abbildung:
Strahlensatz
Sinusberechnungen
Berechnung des Sinus
sinus (Winkel)= Gegenkathete / Hypotenuse
Geben Sie genau 2 Werte an!
Berechnung des Cosinus
cosinus (Winkel)= Ankathete / Hypotenuse
Geben Sie genau 2 Werte an!
Berechnung des Tangens
tangens (Winkel)= Ankathete / Hypotenuse
Geben Sie genau 2 Werte an!
Planimetrie
Dreiecke
Quadrat
Rechteck
Parallelogramm
Raute
Trapez
Reguläres n-Eck
Kreis
Kreissektor
Kreissegment
Kreisring
Ellipse
Dreiecke
Allgemeine Beziehungen
Rechtwinkliges Dreieck
Gleichschenkliges Dreieck
Gleichseitiges Dreieck
allgemeine Beziehungen
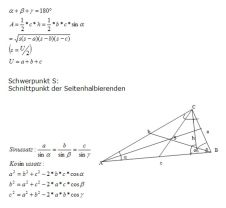
Berechnung aus 2 Seiten und einem Winkel:
Gleichschenkliges Dreieck
a=b alpha=beta
Gleichseitiges Dreieck
a=b=c alpha=beta=gamma=60°Quadrat
Der Schwerpunkt des Quadrates ist der Mittelpunkt Geben sie die Kantenlänge a einRechteck
Parallelogramm
Raute
Trapez
Reguläres n-Eck
Kreis
Kreissektor
Kreissegment
Kreisring
Ellipse
Stereometrie
Würfel
Quader
Pyramide
Pyramidenstumpf
Tetraeder
Gerader Kreiszylinder
Gerader Kreiskegel
Gerader Kreiskegelstumpf
Kugel
Kugelsegment
Kugelzone
Kugelsektor
Ellipsoid
Rotationsparaboloid
Torus
Rotationskörper
Würfel
Quader
Pyramide
Pyramidenstumpf
Tetraeder
Gerader Kreiszylinder
Gerader Kreiskegel
Gerader Kreiskegelstumpf
Kugel
Kugelabschnitt, Kugelsegment oder Kugelkappe
Kugelschicht oder Kugelzone
Kugelausschnitt oder Kugelsektor
Ellipsoid
Rotationsparaboloid
Torus
Rotationskörper
Sinushyperbolicus
Auch hier kommt ein Java-Applet, welches eine Hyperbolische Funktion zeichnet
Zurück zum Anfang
Algebra
Berechnungen (4 Grundrechenarten mit Klammern)
Potenzrechnung
Wurzelziehen
Binomische Formeln
Prozentrechnung
Quadratische Gleichung
Potenzgesetze
Logarithmusgesetze
Potenzrechnung
Wurzelziehen
Binomische Formeln
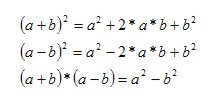
Prozentrechnung
Quadratische Gleichung
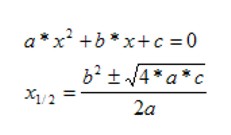
Potenzgesetze
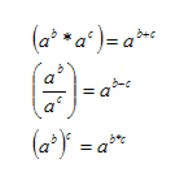
Logarithmusgesetze
1. Einfache Logarithmusberechnung
2. Logarithmusgesetze
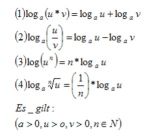
Zurück zum Anfang
Stochastik
Würfeln
Gauß'sche Glockenkurve
Binomialverteilung
Würfeln
Es ist jeweils zu einem Sechstel wahrscheinlich, dass eine der 6 Zahlen vorkommt.
Gaussche Glockenkurve
z.B. bei der Notenverteilung ist die Gaussche Glockenkurve eine Reichtgröße
Binomialverteilung
Zurück zum Anfang
Infinitesimalrechnung
Die Funktion
Folgen
Reihen
Taylor-Reihen
Fourier-Reihen
Grenzwertrechnen
Einfache Ableitungen
Quadratische Ergänzung
HOP TIP und TEP
Ableitung von Brüchen
Kettenregel
L'Hospital
Substitution
Nachdifferenzieren
Kurvendiskussion
Integrieren
Flächenberechnung
Streckenlänge
Integraltabelle
Regel von Simpson
totales Differential
Differentialgleichungen 1. Grades
Die Funktion und ihre Eigenschaften
Unter einer Funktion von einer Variablen versteht man eine Vorschrift, die jedem Element x der Definitionsmenge genau ein Element y der Wertemenge zuordnet. Symbolische Schreibweise y=f(x)
Bezeichnungen:
x: Unabhängige Veränderliche (Variable) oder Argument.
y: Abhängige Veränderliche (Variable) oder Funktionswert.
Allgemeine Eigenschaften
Nullstelle Schnitt bzw. Berührpunkt mit der x-Achse f(x0)=0
Symmetrie: ist , wenn irgendetwas gleich ausschaut
von einer geraden Funktion spricht man bei einer Spiegelsymmetrie zur y-Achse.
f(-x)=f(x)
von einer ungeraden Funktion spricht man, wenn die Funktionskurve punkstsymmetrisch zum Koordinatenursprung ist
f(-x)=-f(x)
Folgen
Folgen sind z.B. Funktionen mit der Definitionsmenge der natürlichen Zahlen.
Unter einer (reellen) Zahlenfolge versteht man eine geordnete Menge reeller Zahlen.
a n = a1. a2. a3, ..... ,an,.... (n ist ein Element der natürlichen Zahlen)
nach Papula
Reihen
Zusammengezählte Folgen
Taylor-Reihen
Fourier-Reihen
Sie spielen einerolle in der Klangerzeugung
Grenzwertrechnen
Eine Feunktion y=f(x) sei in einer Umgebung von x0 definiert. Gilt dann für jede im Definitionsbereich der Funktion liegende und gegen die Stelle x0 konvergierende Zahlen folge xn mit xn ist ungleich zu x0 stets limn -> unendlich f(xn) = g , so heisst g der Grenzwert von y=f(x) für x -> x0limx->x0 f(x) = g
n. Papula
Einfache Ableitungen
Funkionsgraph einer einfachen Funktion
Einfache Kurvendiskussion einer kubischen Funktion
Quadratische Ergänzung
HOP, TIP und TEP
Das sind die Nullstellen der ersten und zweiten Ableitung
Ableitung von Brüchen
Kettenregel
L'Hospital
Substitution
Nachdifferenzieren
Kurvendiskussion
Integrieren
Flächenberechnung
Streckenlänge
Integraltabelle
Regel von Simpson
Totales Differential
Differentialgleichungen ersten Grades
Zurück zum Anfang
Analytische Geometrie
Betrag eines Vektors
Addition
Subtraktion
Skalarprodukt
Kreuzprodukt
Spatprodukt
Ebenen
Zurück zum Anfang
Betrag eines Vektors
Addition eines Vektors
Subtraktion eines Vektors
Skalarprodukt
Multiplikation eines Vektors mit einem Skalar
Skalarprodukt aus Vektorbetrag und Winkel phi
Eigentliches Skalarprodukt aus 2 Vektoren
Kreuzprodukt
Der Betrag des Vektorproduktes entspricht dem Flächeninhalt des von Vektor a und Vektor b aufgepannten ParallelogrammsSpatprodukt
Ebenen
In der Parameterdarstellung
| Gegeben: | Ein Punkt P1 der Ebene E mit dem Ortsvektor r1 und 2 nicht-kollineare Richtungsvektoren a und b der Ebene |
Physik nach Heywang
Mechanik fester Körper
Mechanik der Fluessigkeiten und Gase
Wärmelehre
Schwingungs- und Wellenlehre
Optik
Elektrizitätslehre
Physik der Atomhuelle
Mechanik fester Körper
Physikalische Größen
Bewegungslehre
Dynamik der Kräfte
Gleichgewicht von Kräften
Arbeit, Energie und Leistung
Maschinen
Ergänzende Dynamik
Gravitation
Materialeigenschaften
Zurück zum Anfang
Physikalische Größen
Größen
Messung physikalischer Größen
Größen
1 Newton = 1 N =1kg*m/s^2
1 Meter = 1 m = 100cm
1 Stunde = 1 h = 60 min = 3600 sec
10^12 = Tera
10^9 = Giga
10^6 = Mega
10^3 = Kilo
10^2 = Hekto
10^1 = Deka
10^-1 = Dezi
10^-2 = Zenti
10^-3 = Milli
10^-6 = Micro
10^-9 = Nano
10^-12= Pico
Messung physikalischer Größen
Volumenberechnung
DICHTE
Zurück zum Anfang
Bewegungslehre
Geschwindigkeit und Beschleunigung
Freier Fall
Lotrechter Wurf
Zusammengesetzte Bewegungen
Schiefer Wurf
Drehbewegung
Geschwindigkeit und Beschleunigung
Lineare GeschwindigkeitGeschwindigkeit ist gleich Änderung der Strecke geteilt durch Änderung der Zeit
v= delta s / delta t
Berechnung der linearen Geschwindigkeit:
Beschleunigung
Die Beschleunigung berechnet sich aus der Geschwindigkeitsänderung durch die Zritänderung
Sie ist die 1. Ableitung der Geschwindigkeit und die 2. Ableitung der Strecke jeweils nach der Zeit
Berechnung der Geschwindigkeit aus Anfangsgeschwindigkeit, Beschleunigung und Zeit
Freier Fall
Lotrechter Wurf
Wie hoch kommt ein senkrecht geworfenes Objekt, wie lange dauert das?
Zusammensetzung von Bewegungen
Schiefer Wurf
Kreis- und Drehbewegung
gleichförmige Kreis- und Drehbewegung
beschleunnigte Kreis- und Drehbewegung
Zurück zum Anfang
Dynamik der Kräfte
Grundgestz der Dynamik
Beispiele von Kräften
Grundgesetz der Dynamik
Beispiele von Kräften
Gewichtskraft
Federkraft
Reibung
Gewichtskraft
Federkraft
Reibung
Gleichgewicht von Kräften
Reaktionsprinzip: Mit dem Auftreten einer Kraft ist stets die Entstehung einer Gegenkraft verbunden, die mit der Kraft gleiche Größe, aber entgegengesetzte Richtung hat
Zerlegung und Gleichgewicht von Kräften im gleichen Angriffspunkt
Drehmoment und Hebelgesetz
Schwerpunkt
allgemeine Gleichgewichtsbedingungen
Gleichgewichtsbedingungen und Bezugssystem
Zerlegung und Gleichgewicht von Kräften im gleichen Angriffspunkt
Parallele Kräfte
Nicht parallele Kräfte
Kräftezerlegung
Rechnerische Bestimmung der Resultierenden mehrerer Kräfte
Prallele Kräfte
Die Gesamtkraft mehrere Kräfte bezeichnet man als ihre Resultierende
Greifen mehrere Kräfte in einem Punkt an, so ist die Resultierende bei gleichgerichteten Kräften ihre Summe, bei entgegengesetzt gerichteten Kräften ihre Differenz
2 Kräfte, die im gleichen Punkt,oder in der gleichen Wirkunglinie angreifen, stehen nur dann im Gleichgewicht , wenn sie gleich groß und entgegengerichtet sind.
Nicht parallele Kräfte
Die Resultierende von 2 an einem Punkt unter einem Winkel angreifenden Kräften erhält man nach Gräöße und Richtung als Diagonale in dem durch die beiden Kräfte bestimmten Parallelogramm
Kräftezerlegung
Die Teilkräfte einer Kaft sind die x und y - Richtung die mit der Kraft als Resultierende ein Parallelogramm bilden.Rechnerische Bestimmung der Resultierenden mehrerer Kräfte
Um die resultierende mehrerer Kräfte zu bestimmen, zerlegt man alle Kräfte in einem rechtwinkligen Koordinatensystem in x- und y - Komponenten und bildet daraus die Summe.Excelformular (Passwort: Eingabe)
Drehmoment und Hebelgesetz
Drehmoment = Kraft * HebelarmDer Hebelarm ist die Länge des Lotes vom Drehpunkt auf die Wirkungslinie der Kraft
Drehmoment als Vektor
| An einem Hebel herrscht Gleichgewicht, wenn die Summe der Drehmomente der rechtsdrehenden Kräfte ebenso groß ist, wie die Summe der links drehenden Kräfte |
An einem Hebel herrscht Gleichgewicht, wenn die Summe der Drehmomente 0 ist.
Wirkungen eines Kräftepaars
Ein Kräftepaar erzeugt keine Beanspruchung der Achslager
Drehmoment eines Kräftepaars Ein Kräftepaar stellt unabhängig von der Lage des Drehpunktes das gleiche Dokument dar
Schwerpunkt
Im Schwerpunkt kann man sich die ganze Masse eines Körpers vereint denken
Allgemeine Gleichgewichtsbedingungen
Alle statisch bedingten Aufgaben eines starren Körpers lassen sich mit den allgemeinen Gleichgewichtsbedingungen lösen
Gleichgewichtsbedingungen und Bezugssystem
Die Summe aller Kraftvektoren, so wie aller Drehmomentsvektoren ergibt 0. Das gilt nur für den Beobachter, der sich im selben Bezugssystem befindet. Es gilt:
Die Gleichgewichtsbedingungen sind vom Bezugssystem abhängig
Des weiteren gilt für Kräfte bei gleichförmig bewegetem Bezugssystem z.B. Aufzug:
In zwei Systemen, die sich gegenseitig mit konstanter Geschwindigkeit verschieben, werden alle Kräfte auf irgendeinen Körper in gleicher Größe gemessen. Durch Kräftemessungen kann also nicht entschieden werden, welches Systemsich bewegt.
Für Kräfte bei beschleunigten Systemen gilt:In bezug auf ein beschleunigtes System müssenzu den angreifenden Kräften noch die Trägheitskraäfte hinzugefügt werden, damit das Grundgesetz der Dynamik auch in diesem Bezugssystem seine Gültigkeit behält.
Bei G-m*g=0 befindet sich ein Körper im zustand der Schwerelosigkeit.
Beschleunigte Bewegungen können mit hilfe der Gleichgewichtsbedingungen nach dem Prinzip von d'Alembert berechnet werden
Ein Bezugssystem , in dem zur Beschreibung einer gleichförmigen Bewegung keine Trägheitskräfte eingeführt werden müssen, nennt man Inertialsystem.
Ein mit der Erdoberfläche verbundenes Bezugssystem kann man nahezu, weil die Trägheit nicht messbar ist, als Inertialsystem bezeichnet werden.
Arbeit, Energie und Leistung
Energiarten der Mechanik
Satz von der Erhaltung der Energie
Leistung und Wirkungsgrad
Energiearten der Mechanik
Mechanische Arbeit und ihre Berechnung
Mechanische Arbeit wird verrichtet, wenn eine Kraft längs eines Weges einen Widerstand überwindet, sie wird gemessen durch das Produkt aus der Kraft i und dem Weg
Berechnung der Arbeit:
Hubarbeit wird verrichtet, wenn ein Gegenstand hochgehoben wird entspricht auch der Energie der Lage
Berechnung der Hubarbeit = potentielle Energie
Beim Verschieben eines Gegenstandes auf horizontaler Ebene muss nur die Reibungskraft auf den Weg überwunden werden. Das ist die sogenannte Verschiebearbeit.
Nun zur Berechnung der potentiellen Energie einer gespannten Feder
Berechnung der kinetischen Energie
Satz von der Erhaltung der Energie
Erhaltung der mechanischen Arbeit:
Durch keine mechanische Vorrichtung lässt sich Arbeit geweinnen. Bei Vernachlässigung der Reibungsverluste sind aufgewandte und erzielte Arbeit gleich. Die mechanische Arbeit bleibt erhalten.
Energieerhaltungssatz
Bei keiner Vorrichtung und keinem Vorgang kann Energie erzeugt werden oder verlorengehen. Energie kann nur umgewandelt werden
Delta E = W
Berechnung der Endgeschwindigkeit eines Körpers, der ohne wesentliche Reibung Höhe verliert.
Leistung und Wirkungsgrad
Leistung
Momentanleistung
Wirkungsgrad
Leistung
Die (mittlere) Leistung während eines Zeitintervalls ist der Quotient aus der Arbeit und der für sie benötigten ZeitLeistung
Momentanleistung
Wirkungsgrad
Leistung
Momentanleistung
Wirkungsgrad
Maschinen
Ergänzende Dynamik
allgemeine Grundsätze der Dynamik
Kraftstoß, Impuls, Impulssatz
Zentripetal- und Zentrifugalkraft
Corioliskraft
Beschleunigte Drehbewegung um eine Achse
gleichzeitiger Ablauf von Translation und Rotation (Zykloide)
allgemeine Grundsätze der Dynamik
Zusammenfassung der Newtonschen Axiome
Erhaltungssätze
(Ir)Reservibilität
Kausalität
Zusammenfassung der Newtonschen Axiome
Aus dem Trägheitsgesetz geht hervor, dass bei keinem Körper ohne Einwirkung einer Kraft eine Bewegung besteht, sondern dass bei ihm der vorhandene Bewegungszustand erhalten bleibt. Wenn aber an einem Körper Kräfte angreifen, deren Resultierende nicht Null ist, dann entsteht eine Beschleunigung, die sich nach dem Grundgesetz der Dynamik berechnen lä:sst. Das Grundgesetz lässt die Wirkung einer Kraft auf den Körper, an dem sie angreid, berechnen; es macht aber keine Aussage über die Rückwirkung auf den Körper, von dem sie ausgeht. Deshalb benötigt man auch eine Aussage über die Wechselwirkung mehrerer Massen. Diese finden wir im Reaktionsprinzip, wonach jeder Körper, der eine Kraft ausübt, selbst von einer ebenso großen Gegenkraft getroffen wird.
Es ist das große Verdienst Isaac Newtons, in diesen drei Gesetzen die Grundlage der gesamten Mechanik erkannt zu haben. Alle drei Gesetze sind durch die Erfahrung oder durch Experimente gesichert. Newton setzte ihre Gültigkeit in seinem Werk über die mathematischen Prinzipien der Naturwissenschaft (philosophiae naturalis principia mathematica ) voraus und leitete aus ihnen mit mathematischen Hilfsmittelnb alle weiteren Gesetze ab. Auf diese Weise baut sich die gesamte Mechanikauf diesen drei Gesetzen auf. Da ihre Richtigkeit vorausgesetzt, also gleichsam gefordert wird, bezeichnet man sie als die Newtonschen Axiome der Mechanik. (griechisch : axioein = fordern)
Erhaltungssätze
Der Satz von der Erhaltung der Energie gestattet bei reibungsarmen Vorgängen Aussagen zu machen, selbst wenn man den Ablauf der Vorgänge im einzelnen nicht kenn. Der Erhaltungssatz verschafft also einen raschen Übergang über zahlreiche Vorgänge. Dies gilt auchvon anderen Erhaltungssätzen, die in der Physik auftreten. Die tägliche Erfahrung lässt uns z.B. den Satz von der Erhaltung der Masse als nahezu selbstverständliches Gesetz erscheinen. Im folgenden Abschnitt wird ein weiterer Erhaltungssatz aus der Mechanik abgeleitet werden. Auch in anderen Gebieten der Physik gibt es noch Erhaltungssätze, die bei der Forschung vor allembei der über die Elementarteilchen(der kleinsten Teilchren, aus denen sich alle MAterie und Energie zusammensetzt) eine große Bedeutung erlangt haben.
(Ir)Reservibilität
Nach dem Satz der Energie wird die Arbeit, die aufgewendet wird, um einen Körperreibungslos von einem Punkt an einen anderen zu bringen, in kinetische und potenzielle Energie umgewandelt. Wenn der Körper zum Ausgangspunkt zurückgebracht wird, werden die Energien wieder frei, so dass der ursprüngliche Zustand wieder entsteht. Ein solcher Vorgang ist umkehrbar und reversibel. Dies gilt aber nicht mehr, wenn ein Teil der aufgewandten Arbeit nicht als potentielle oder kinetische Energie gespeichert wird, lässt sie sich nicht mehr in mechanische Arbeit zurückverwandeln. Dann lässt sich ein Vorgang nicht mehr umkehren, er ist irreversibel. Da alle wirklich ablaufende Vorgänge mit Reibung verbunden sind, verlaufen sie irreversibel, so dass es streng genommenkeine reversiblen Vorgänge gibt.
Kausalität
Wenn sich zwei Körper im gleichen Zustand befinden und an ihnen die gleichen Kräfte angreifen, so entsteht bei ihnen auch der gleiche mechanische Vorgang. Diese Erkenntnis kann man in folgendem Satz formulieren:
Gleiche Ursachen haben stets gleiche Wirkungen.
Da die mechanischen Gesetze bekannt sind,müsste man aus einem Anfangszustand , bei dem alle Eigenschaften und Begleitumstände bekannt sind, den Folgezustand berechnen können. Lediglich die Unmöglichkeit die Begleitumstände hinreichend zu erfassen, verhindert eine sichere Voraussage . Diesen Zusammenhang zwischen Ursache und Wirkung bezeichnet man als Kausalität (lat.: causa = Ursache). Sie ist nicht nur in der MEchanik, sondern in der ganzen Physik erfüllt, wenn die beteiligten Körper nicht zu kleine Massen besitzen und wenn nicht zu kleine Energiebeträge ausgetauscht werden.
Im atomaren Bereich oder bei spezielleren Vorgängen kann über das Gesetz der Kausalität nicht mehr alles erfasst werden.
Kraftstoß, Impuls, Impulssatz
Zentripetal- und Zentrifugalkraft
Corioloskraft
Beschleunigte Drehbewegung um eine Achse
gleichzeitiger Ablauf von Translation und Rotation (Zykloide)
Gravitation
Materialeigenschaften
Mechanik der Flüssigkeiten und Gase
Wärmelehre
Schwingungs - und Wellenlehre
Optik
Elektrizitaetslehre
Elektrische Grunderscheinungen
Elektrostatik
Elektrizitätsleitung in Metallen
Elektrizitätsleitung in Elektrolyten
Elektrizitätsleitung in Vakuum und Gasen
Elektrische Grunderscheinungen
Ruhende Ladung
Bewegte Ladung
Ruhende Ladung
- Gleichnamige Ladungen stoßen sich ab, ungleichnamige ziehen sich an
- Die Kräfte nehmen mitwachsendem abstand stark ab.
Elektronenmangel ergibt eine positive, Elektronenüberrschuss eine negative Ladung
Messen kann man die Ladung mit dem Elektroskop!
Bewegte Ladung
Bewegte Ladungen stellen einen Strom dar.
Das Ampere ist die Stärke eines zeitlich unveränderlichen Stromes, der durch 2 im Vakuum im
Abstand von 1 Meter voneinander angeordnete geradlinige, unendlich lange Leiter von je
vernachlässigbar kleinem kreisförmigen Querschnitt fließend, zwischendiesen Leitern je
1 MeterLeiterlänge die Kraft 2* 10^-7 Newton hervorruft.
Physiik der Atomhülle
Chemie
Grundlagen der Stöchiometrie (Molberechnungen)
Aufstellen von Reaktionsgleichungen
OrganikABC
Grundlagen der Stöchiometrie
Molare Masse
Stoffmenge
Masse
Konzentration
molares Volumen
Molare Masse
Stoffmenge
aus Masse und molarer Masse
aus Konzentration und Volumen
Masse
Konzentration
Molares Volumen
Aufstellen von Reaktionsgleichungen
Salze
Salze
Verfahrenstechnik
Allgemeine Grundlagen
Mechanische Strömungslehre
Lagern und Speichern
Kennzeichnung, Zerkleinerung und Transport von Feststoffen
Technische Strömungslehre
Fördern von Flüssigkeiten und Gasen
Trennen disperser Systeme
Mechanische Stoffvereinigung
Wärmeübertragung
Beheizen und Kühlen
Stoffübertragung
Trocknung
Destillation
Sorption
Extraktion
Stoffumwandlung in Reaktoren
Allgemeine Grundlagen
Allgemeine Formelzeichen
Stoff- Wärme und Inpulsübertragung
Ähnlichkeitslehre
Diskontinuierliche und Kontinuierliche Betriebsweise
Stoff- und Energiebilanzen
Zurück zum Anfang
Allgemeine Formelzeichen
Allgemeine Formelzeichen
Stoff- Wärme und Impulsübertragung
Konvektionsströme
Leitströme
Übergangsströme
Konvektionsströme
Hier gilt: Konvektionsstrom = Dichte x Fläche x Strömungsgeschwindigkeit
Berechnung eines Massestromes
Berechnung des Komponentenstroms
Berechnung des Wärmestroms
Mechanische Strömungslehre
Stoffeigenschaften von Flüssigkeiten und Gasen
Hydrostatik
Aerostatik
Inkompressible Strömungen
Kompressible Sttrömungen
Strömungsmeßtechnik
Stoffeigenschaften von Flüssigkeiten und Gasen
Dichte
Schallgeschwindigkeit
Viskosität
Thermische Stoffwerte
Oberflächenspannung und Kapillarität
Dichte
Definitionen
Dichte von Flüssigkeiten
Dichte von Gasen und Dämpfen
Dichte von Luft
Definitionen
Der Kehrwert der Dichte wird als spezifisches Volumen bezeichnet.
Dichte von Flüssigkeiten
Die Temperaturabhängigkeit der Dichte kann durch den isobaren Wärmeausdehnungskoeffizienten beta p ausgedrückt werden.
Flüssigkeiten besitzen wie feste Körper eine geringe Elastizität.
Nimmt man nach dem Hookeschen Gesetz einen linearen Zusammenhang zwischen Volumen- und Druckänderung an, kann man die Dichte bei bestimmten Druck berechnen!
Dichte von Gasen und Dämpfen
Hydrogeologie
Niederschlag
Verdunstung
Niederschlag
Wasserbilanzgleichung
Gebietsniederschlagshoehe mit Hilfe von Thiessen Polygonen
Niederschlagshoehen mit Isohyeten
Wasserbilanzgleichung (hydrologische Grundgleichung)
Modifizierte Grundgleichung
Wasserbilanzgleichung nach LIEBSCHER
Gebietsniederschlagshöhen
Niederschlagshöhen in Gebieten mit starkem Oberflächenrelief
Isohyeten-Karten - Methode
Zunächst benötigen Sie die Niederschlagshöhen der benachbarten Isohyeten (N2 < N1)
Verdunstung
Wirtschaft
Grundwissen Industriekaufleute
Grundlagen der Wirtschaft alphabetisch
Grundwissen Industriekaufleute
wirtschaftliche Zielsetzungen
wirtschaftliche Zielsetzungen
Rentabilität
Wirtschaftlichkeit
Produktivität
Grundlagen der Wirtschaft alphabetisch
ABC-Analyse
Abschreibungen
Aktien
Angebotsvergleich
Annuitätenmethode
Äquivalenzziffernkalkulation
BAB (Betriebsabrechnungsbogen)
Barwertmethode
Baufinanzierung
Bestellmenge
Bezugsrecht
Bilanzkennzahlen
Break-even-Analyse
Cashflow
Darlehen
Deckungsbeitragsrechnung
Differenzkalkulation
Diskontrechnen
Dreisatz
Effektivzins
Festverzinsliche Wertpapiere
Handelskalkulation
Herstellkosten
Indexzahlen
Industrielle Kalkulation
Interner Zinsfuß
Investitionsfinanzierung
Investitionsrechnungen
Kalkulatorische Kosten
Kapitalrückflussrechnung
kaufmännische Zinsrechnung
Kennzahlen
Kurs-Gewinn-Verhältnis
Kommissionsgeschäfte
Kontokorrentkredit
Kosten und Beschäftigung
Lagerkennzahlen
Leasing
Lohnformen
Mittelwerte
Produktivität und Wirtschaftlichkeit
Prozentrechnung
Prozesskostenrechnung
Rentabilität
Return on Investment (ROI)
Rückwärtskalkulation
Statistik
Stichproben
Streuungsmaße
Target Kosting
Terminrechnung
Trendanalyse
Umsatzentwicklung und Umsatzanalyse
Verteilungsrechnung
Vorkalkulation
Währungsrechnen
Wertschöpfungsrechnen und Shareholder Value
Zinsen
Zinseszinsrechnen
Zuschlagsrechnung
Wichtige Formeln im Überblick
Betriebsabrechnungsbogen
BAB Excel-Datei
Passwort = test
Zurück zum Anfang
Applettest
JavaScripttest
SVG-Test
Informatik
Zahlensysteme
Logik
Größen, Formelzeichen und Einheiten"
Akustik
Optik
Taktfrequenz
Zahlensysteme
dezimal->binär
dezimal->hexadezimal
binär->dezimal
binär->hexadezimal
hexadezimal->dezimal
hexadezimal->binär
dezimal -> binär
Logik
Wahrheitstabellen
Rechenregeln
Wahrheitstabellen
Rechenregeln
Rechenregeln zur Aussagenlogik
Größen, Formelzeichen und einheiten
Akustik
Optik
Taktfrequenz
Regeltechnik
In der Regeltechnik soll der Istwert durch eine Stellgröße einem Sollwert angeglichen werden.
Dabei können Störgrößen, wie Dunkelheit, Reibung oder Konfliktpotential z.B. durch Entgegensteuern vermieden werden.